

Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and are commonly used to represent a complex number. Some of the examples of real numbers are 23, -12, 6.99, 5/2, π, and so on. In this article, we are going to discuss the definition of real numbers, the properties of real numbers and the examples of real numbers with complete explanations.


Table of contents:
Real numbers can be defined as the union of both rational and irrational numbers. They can be both positive or negative and are denoted by the symbol “R”. All the natural numbers, decimals and fractions come under this category. See the figure, given below, which shows the classification of real numerals.
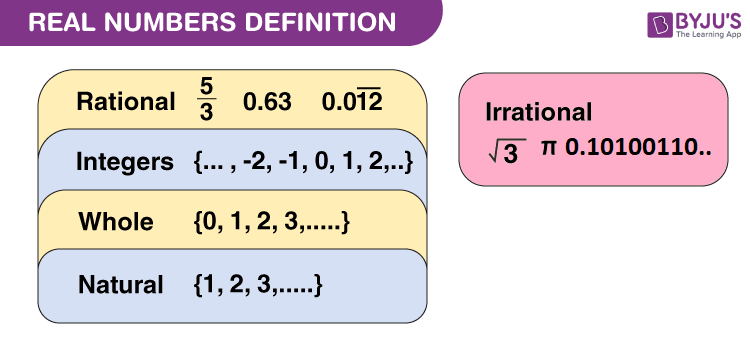
Read More:
The set of real numbers consists of different categories, such as natural and whole numbers, integers, rational and irrational numbers. In the table given below, all the real numbers formulas (i.e.) the representation of the classification of real numbers are defined with examples.
| Category | Definition | Example |
|---|---|---|
| Natural Numbers | Contain all counting numbers which start from 1. |
The chart for the set of real numerals including all the types are given below:
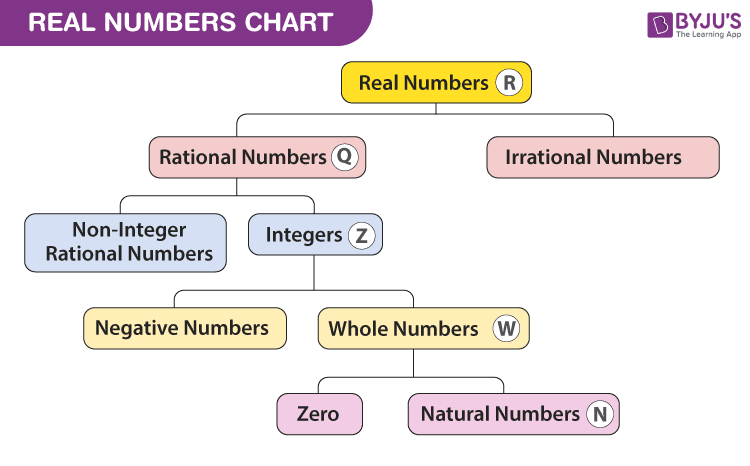
The following are the four main properties of real numbers:
Consider “m, n and r” are three real numbers. Then the above properties can be described using m, n, and r as shown below:
If m and n are the numbers, then the general form will be m + n = n + m for addition and m.n = n.m for multiplication.
If m, n and r are the numbers. The general form will be m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication.
For three numbers m, n, and r, which are real in nature, the distributive property is represented as:
m (n + r) = mn + mr and (m + n) r = mr + nr.
There are additive and multiplicative identities.

| Learn More About Real Number Properties | |
|---|---|
| Commutative Property | Associative Property |
| Distributive Property | Additive Identity and Multiplicative Identity |
Find five rational numbers between 1/2 and 3/5.
We shall make the denominator same for both the given rational number
(1 × 5)/(2 × 5) = 5/10 and (3 × 2)/(5 × 2) = 6/10
Now, multiply both the numerator and denominator of both the rational number by 6, we have
(5 × 6)/(10 × 6) = 30/60 and (6 × 6)/(10 × 6) = 36/60
Five rational numbers between 1/2 = 30/60 and 3/5 = 36/60 are
31/60, 32/60, 33/60, 34/60, 35/60.
Write the decimal equivalent of the following:
(i) 1/4 (ii) 5/8 (iii) 3/2
(i) 1/4 = (1 × 25)/(4 × 25) = 25/100 = 0.25
(ii) 5/8 = (5 × 125)/(8 × 125) = 625/1000 = 0.625
(iii) 3/2 = (3 × 5)/(2 × 5) = 15/10 = 1.5
What should be multiplied to 1.25 to get the answer 1?
Solution: 1.25 = 125/100
Now if we multiply this by 100/125, we get
125/100 × 100/125 = 1
In real numbers Class 9, the common concepts introduced include representing real numbers on a number line, operations on real numbers, properties of real numbers, and the law of exponents for real numbers. In Class 10, some advanced concepts related to real numbers are included. Apart from what are real numbers, students will also learn about the real numbers formulas and concepts such as Euclid’s Division Lemma, Euclid’s Division Algorithm and the fundamental theorem of arithmetic in class 10.
Keep visiting BYJU’S to get more such Maths lessons in a simple, concise and easy to understand way. Also, register at BYJU’S – The Learning App to get complete assistance for Maths preparation with video lessons, notes, tips and other study materials.


Natural numbers are all positive integers starting from 1 to infinity. All natural numbers are integers but not all the integers are natural numbers. These are the set of all counting numbers such as 1, 2, 3, 4, 5, 6, 7, 8, 9, …….∞.
Real numbers are numbers that include both rational and irrational numbers. Rational numbers such as integers (-2, 0, 1), fractions(1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.
Zero is considered to be both a real and an imaginary number. As we know, imaginary numbers are the square root of non-positive real numbers. And since 0 is also a non-positive number, therefore it fulfils the criteria of the imaginary number. Whereas 0 is also a rational number, which is defined in a number line and hence a real number.
No, there are no real numbers that are neither rational nor irrational. The definition of real numbers itself states that it is a combination of both rational and irrational numbers.
Yes, because a complex number is the combination of a real and imaginary number. So, if the complex number is a set then the real and imaginary numbers are the subsets of it.
The properties of real numbers are:
Commutative Property
Associative Property
Distributive Property
Identity Property
Yes, √3 is a real number. We know that a real number is a combination of both rational and irrational numbers. Since √3 is an irrational number, we can also say that √3 is a real number.
No, 3i is not a real number, as it has an imaginary part in it.
The subsets of real numbers include rational numbers, irrational numbers, natural numbers, and whole numbers.
Test your Knowledge on Real Numbers

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below